
Les abscisses et les ordonnées représentent des concepts fondamentaux en mathématiques et dans de nombreuses disciplines scientifiques. Comprendre leurs rôles et leur utilité est essentiel, que ce soit dans le domaine de la géométrie, de l’algèbre, de la physique ou même dans les sciences sociales. Cet article explore en profondeur chacun de ces aspects, offrant une vision complète de l’importance des axes dans le plan cartésien.
Le repère cartésien : fondements et définitions
Le repère cartésien est un cadre de travail crucial dans lequel l’on peut situer des points selon deux dimensions. Ce système est constitué de deux axes perpendiculaires : l’axe des abscisses (horizontal) et l’axe des ordonnées (vertical). Ces axes se croisent en un point d’origine, souvent désigné par (0, 0). La compréhension de ce système est essentielle pour toute représentation graphique.
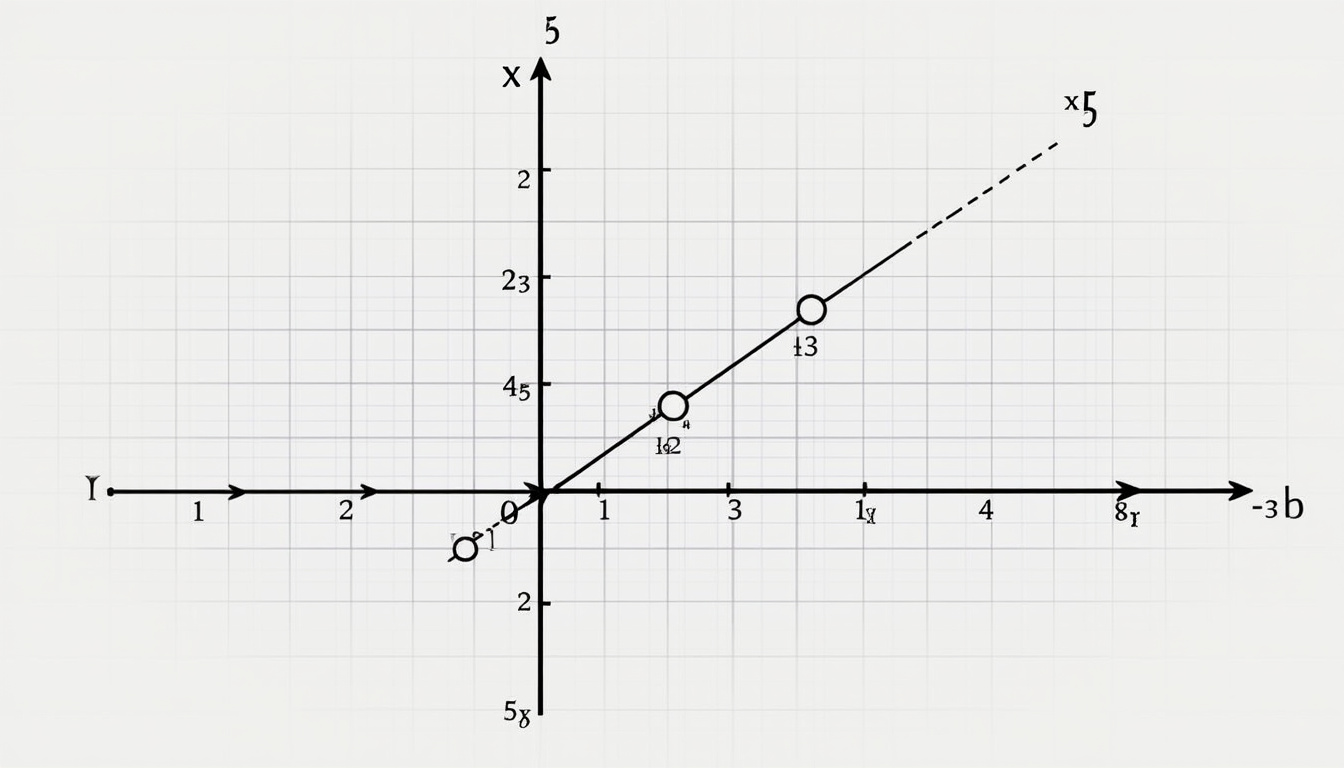
Les caractéristiques du repère cartésien
Dans un repère cartésien, chaque point est déterminé par ses coordonnées qui se présentent sous la forme (x, y) où :
- x représente la valeur sur l’axe des abscisses, indiquant la position horizontale.
- y représente la valeur sur l’axe des ordonnées, indiquant la position verticale.
Cette notation permet une lecture simple et intuitive des positions des points.
Pourquoi utiliser le repère cartésien ?
Le repère cartésien est utilisé pour plusieurs raisons clés :
- Visualisation : Il permet de représenter graphiquement des données, facilitant ainsi leur interprétation.
- Calculs : Les systèmes algébriques peuvent être simplifiés à l’aide de graphes,rendant des calculs complexes plus digestes.
- Interprétation géométrique : Les propriétés géométriques des formes sont plus aisément observables lorsque ces dernières sont tracées sur un graphique.
Abscisse : définition et utilisation
L’abscisse est définie comme la coordonnée horizontale d’un point dans le plan cartésien. Elle indique la distance entre ce point et l’axe des ordonnées. Comprendre comment lire et interpréter l’abscisse est essentiel pour travailler avec des graphes et des fonctions.
Exemples d’abscisses
Considérons un point P avec une coordonnée d’abscisse de 4, noté P(4, y). Cela signifie que P se trouve à quatre unités à droite de l’origine. À l’inverse, un point Q avec une abscisse de -3, noté Q(-3, y), se trouve trois unités à gauche de l’origine. Cette perspective ponctuelle permet de mieux appréhender l’organisation des points dans l’espace.
Applications de l’abscisse
L’abscisse joue un rôle essentiel dans divers domaines :
- Géométrie : Tracing de figures et calcul des distances.
- Algèbre : Résolution d’équations et représentations graphiques.
- Statistiques : Représentation de données dans des histogrammes.
Ordonnée : définition et importance
L’ordonnée, quant à elle, est la coordonnée verticale d’un point. Ce qui la distingue de l’abscisse, c’est son lien avec l’axe des abscisses. Une compréhension claire de l’ordonnée permet non seulement de comprendre les positions, mais aussi d’interagir avec des fonctions mathématiques plus complexes.

Exemples d’ordonnées
Par exemple, le point R(2, 5) possède une ordonnée de 5, signifiant qu’il est situé à cinq unités au-dessus de l’origine. Inversement, le point S(3, -2) indique une position deux unités en dessous de l’origine.
Applications de l’ordonnée
Les usages de l’ordonnée sont variés et essentiels dans plusieurs disciplines :
- Fonctions : La courbe d’une fonction est tracée avec l’ordonnée pour représenter des valeurs en fonction de l’abscisse.
- Sciences : Graphes de phénomènes physiques, comme la vitesse ou la force.
- Statistique : Analyse des tendances sur un graphique.
Liens entre abscisse et ordonnée
Les concepts d’abscisse et d’ordonnée sont interdépendants. Lorsque l’on connaît l’un, il est souvent possible de déduire l’autre, surtout dans le contexte des fonctions. Par exemple, pour une fonction f(x), la notation f(a) indique l’ordonnée d’un point lorsque l’abscisse est a.
Utilisation des coordonnées
Les coordonnées (x, y) d’un point possèdent plusieurs fonctionnalités :
- Localisation : Identifier la position exacte d’un point dans un graphique.
- Analyse des graphes : Identifier les intersections, les maxima et minima, ainsi que la tendance générale des fonctions.
- Conversion : Rendre possible la conversion entre des systèmes de coordonnées variés, y compris les coordonnées polaires.
Interpréter les points sur un graphique
Interpréter des points sur un graphique repose sur la capacité à comprendre les relations entre abscisse et ordonnée. Cela inclut des compétences telles que le repérage graphique et le calcul des intersections.
Exemples d’interprétation
La lecture d’un graphique pour découvrir une valeur ou des points d’intersection nécessite précisément la méthode suivante :
- Identifiez l’abscisse ou l’ordonnée.
- Tracez une ligne perpendiculaire de sorte à rejoindre la courbe.
- Établissez des parallèles pour déterminer les coordonnées demandées.
Importance des axes dans les fonctions mathématiques
Les axes des abscisses et ordonnées sont cruciaux dans l’étude des fonctions mathématiques. Chaque valeur sur l’axe des abscisses représente une entrée dans une fonction, tandis que l’ordonnée représente la sortie correspondante. Cette structure est essentielle dans des domaines variés tels que les mathématiques avancées, la physique ainsi que l’économie.
Analyser les variations d’une fonction
En étudiant les coordonnées sur la courbe d’une fonction, il est possible d’examiner les variations. Cela nécessite :
- Identifiant les zones croissantes et décroissantes : Établir des intervalles selon la direction de la fonction.
- Détermination des extrema : Calculer les maxima et minima.
Exercices pratiques
Une façon d’apprendre ces concepts est de s’engager dans des exercices pratiques qui renforcent leur utilisation. Considérons quelques points pour lesquels il faut identifier les coordonnées :
| Point | Coordonnées |
|---|---|
| A | (3, 4) |
| B | (-3, 5) |
| C | (5, 7) |
Les étudiants peuvent pratiquer leur lecture du plan cartésien et affiner leurs compétences en traçant des graphiques.
FAQ sur abscisse et ordonnée
Q: Qu’est-ce qu’une abscisse ?
A: L’abscisse est la coordonnée horizontale d’un point dans un repère cartésien, indiquant sa position à partir de l’axe des ordonnées.
Q: Comment trouver l’ordonnée correspondante d’une abscisse donnée ?
A: On trace une ligne verticale à partir de l’abscisse sur le graphique jusqu’à ce qu’elle croise la courbe, puis on lit la valeur sur l’axe des ordonnées.
Q: Pourquoi est-il important de comprendre ces concepts en mathématiques ?
A: Comprendre les abscisses et ordonnées est fondamental pour le tracé de graphiques, l’analyse de données, et la résolution d’équations mathématiques.
Q: Comment ces concepts sont-ils utilisés en physique ?
A: En physique, les graphes de mouvement et d’autres relations sont souvent tracés sur un plan cartésien pour visualiser et analyser des phénomènes.
Q: Les abscisses et ordonnées peuvent-elles être négatives ?
A: Oui, dans un plan cartésien, les coordonnées peuvent être négatives, ce qui permet de représenter des points situés à gauche ou en dessous de l’origine.




